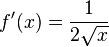quien invento la raiz cuadrada?
Ya en la epoca de los Egipcios, aparecen documentos como el papiro de Ajmeed en el que se muestra como obtener raices cuadradas. Por tanto podemos atribuir a los egipcios el invento de la raiz cuadrada, aunque verdaderamente su origen se pierde en los tiempos
David Eugene Smith, en History of Mathematics, dice acerca de la situación existente:
"En Europa esos métodos (para encontrar el cuadrado y la raíz cuadrada) no aparecieron antes de Cataneo (1546). Él dio el método de Aryabhata para determinar la raíz cuadrada".[3]
Según Julio Rey Pastor y José Babini, Catald calcula en 1613 raíz cuadrada aproximando por fracciones continuas, como aparece en la obra común Historia de la Matemática.
El símbolo de la raíz cuadrada fue introducido en 1525 por el matemático Christoph Rudolff para representar esta operación[4] [5] que aparece en su libro Coss, siendo el primer tratado de álgebra escrito en alemán vulgar. El signo no es más que una forma estilizada de la letra r minúscula para hacerla más elegante, alargándola con un trazo horizontal, hasta adoptar el aspecto actual, que representa la palabra latina radix, que significa raíz. También se conjetura que pudiese haber surgido de la evolución del punto que en ocasiones se usaba anteriormente para representarlo, donde posteriormente se le habría añadido un trazo oblicuo en la dirección del radicando.
Tiempo atrás, varios matemáticos vieron la necesidad de idear números que representasen la raíz cuadrada de números negativos para poder resolver todas las ecuaciones de segundo grado, pero no será hasta 1777 cuando Euler simbolice la raíz cuadrada de -1 con la letra i, dando así cabida al desarrollo de los números complejos.
la raiz cuadrada
BIENVENIDOS A NUESTRO BLOG SOMOS ALAN QUIROGA Y KEVIN JOFRE ESPERO QUE LES GUSTE NUESTRO BLOG Y ESPERAMOS QUE APRENDAN A RESOLVER LA RAIZ CUADRADA
jueves, 15 de mayo de 2014
martes, 15 de abril de 2014
martes, 25 de marzo de 2014
Aproximaciones enteras
Los diseñadores de presentaciones de videojuegos tienen a veces necesidad de construir tablas de partes enteras de las raíces cuadradas de los enteros naturales. Las primeras dadas por:
| CUADRADO | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ... | 15 | 16 | 17 | ... | 24 | 25 | 26 | 27 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RAÍZ | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | ... | 3 | 4 | 4 | ... | 4 | 5 | 5 | 5 |
Una observación de los primeros términos ponen de manifiesto que la construcción para de enteros en enteros, y se salta sucesivamente un incremento de manera regular. Más precisamente:
- El cero es repetido una vez.
- El 1 tres veces.
- El 2 cinco veces
- El 3 siete veces.
- El 4 nueve veces.
El número de veces que el entero n es repetido es el n-ésimo entero impar. La prueba reside sobre la identidad siguiente:
Fracciones continuas
Uno de los resultados más intrigantes del estudio de números irracionales como fracciones continuas fue obtenido por Joseph-Louis Lagrange cerca de 1780. Lagrange descubrió que la raíz cuadrada de cualquier número entero positivo no cuadrado se puede representar por una fracción continua periódica, es decir, donde ocurre cierto patrón de dígitos repetidamente en los denominadores. En un sentido estas raíces cuadradas son números irracionales mucho más simples, porque pueden ser representadas con un patrón de dígitos de repetición simple.
Radicales jerarquizados cuadrados
En diferentes contextos se utilizan radicales de la forma
que en algunos casos puede ser escritos en la forma
lo que es factible si sólo si x + y = A, xy = B .7 8 Las expresiones anteriores se denominan radicales jerarquizados.
La identidad  implica que
implica que  , y por repeticiones sucesivas:
, y por repeticiones sucesivas:
 implica que
implica que  , y por repeticiones sucesivas:
, y por repeticiones sucesivas:
Por razones análogas se obtiene:
;
o que
;
Si r es una entidad estrictamente superior a uno,
Esta forma de expresar números mediante la repetición sucesiva de números contenidos dentro de raíces cuadradas puede tener diversas aplicaciones como la resolución de algunos tipos de ecuación o la expresión de algunos números famosos como el número áureo o el número pi9 .
Irracionalidad de las raíces cuadradas
Una propiedad importante de la raíz cuadrada de los números enteros es que, si estos no son cuadrados perfectos, sus raíces son siempre números irracionales, que son números no expresables como el cociente de dos números enteros. Es decir, la raíz cuadrada de un número entero siempre será entero o irracional, nunca un número racional.
Cualquier número entero puede ser expresado como el producto de una serie de factores primos elevados a diversos exponentes. De ser todos pares, las propiedades de la potenciación permiten reducir la raíz a un número natural. Sólo si uno o más de los factores tiene un exponente impar la raíz no es natural.
Si  fuera racional se debería poder expresar como
fuera racional se debería poder expresar como  con p, q enteros y primos entre sí. Elevando al cuadrado ambas partes se obtiene que
con p, q enteros y primos entre sí. Elevando al cuadrado ambas partes se obtiene que  , lo que es absurdo, pues a un lado queda al menos un factor primo con exponente impar mientras que, al otro lado de la igualdad, tanto
, lo que es absurdo, pues a un lado queda al menos un factor primo con exponente impar mientras que, al otro lado de la igualdad, tanto 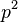 como
como  se expresan en función de producto de primos elevados a exponentes necesariamente pares.
se expresan en función de producto de primos elevados a exponentes necesariamente pares.
 fuera racional se debería poder expresar como
fuera racional se debería poder expresar como  con p, q enteros y primos entre sí. Elevando al cuadrado ambas partes se obtiene que
con p, q enteros y primos entre sí. Elevando al cuadrado ambas partes se obtiene que  , lo que es absurdo, pues a un lado queda al menos un factor primo con exponente impar mientras que, al otro lado de la igualdad, tanto
, lo que es absurdo, pues a un lado queda al menos un factor primo con exponente impar mientras que, al otro lado de la igualdad, tanto 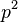 como
como  se expresan en función de producto de primos elevados a exponentes necesariamente pares.
se expresan en función de producto de primos elevados a exponentes necesariamente pares.
Por una reducción al absurdo llegaron los pitagóricos a la demostración de la irracionalidad de la raíz cuadrada de 2, atribuida a Hipaso de Metaponto, un discípulo de Pitágoras. La idea, contraria a lo esperado en la matemática de entonces, supuso la denominada crisis de los inconmensurables de la filosofía pitagórica.
No obstante, es exactamente la longitud de la diagonal de un cuadrado cuyo lado mide 1, siendo fácil la construcción gráfica de la raíz. Por ello buena parte de la matemática helénica se centró en la geometría aplicada como forma de calcular gráficamente valores como ése. Teodoro de Cirene llegó a la espiral que lleva su nombre, que permite representar gráficamente cualquier raíz, y posteriormente Euclides llegó a un método más general.
Propiedades generales
La función raíz cuadrada  es una función cuyo dominio e imagen es el conjunto
es una función cuyo dominio e imagen es el conjunto  (el conjunto de todos los números reales no negativos). Esta función regresa un valor que es único. Las siguientes propiedades de la raíz cuadrada son válidas para todos los números reales no negativos x, y:
(el conjunto de todos los números reales no negativos). Esta función regresa un valor que es único. Las siguientes propiedades de la raíz cuadrada son válidas para todos los números reales no negativos x, y:
 es una función cuyo dominio e imagen es el conjunto
es una función cuyo dominio e imagen es el conjunto  (el conjunto de todos los números reales no negativos). Esta función regresa un valor que es único. Las siguientes propiedades de la raíz cuadrada son válidas para todos los números reales no negativos x, y:
(el conjunto de todos los números reales no negativos). Esta función regresa un valor que es único. Las siguientes propiedades de la raíz cuadrada son válidas para todos los números reales no negativos x, y: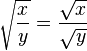

- La función raíz cuadrada, en general, transforma números racionales en números algebraicos;
 es racional si y sólo si
es racional si y sólo si  es un número racional que puede escribirse como fracción de doscuadrados perfectos. Si el denominador es
es un número racional que puede escribirse como fracción de doscuadrados perfectos. Si el denominador es 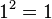 , entonces se trata de un número natural. Sin embargo,
, entonces se trata de un número natural. Sin embargo, 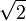 es irracional.
es irracional. - La interpretación geométrica es que la función raíz cuadrada transforma la superficie de un cuadradoen la longitud de su lado.
- Contrariamente a la creencia popular,
 no necesariamente es igual a
no necesariamente es igual a  . La igualdad se mantiene sólo para los números no negativos
. La igualdad se mantiene sólo para los números no negativos  , pero cuando
, pero cuando 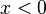 ,
,  es un número positivo, y entonces
es un número positivo, y entonces 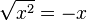 . Por lo tanto,
. Por lo tanto,  para todos los números reales
para todos los números reales  (véase valor absoluto).
(véase valor absoluto). - Suponga que
 y
y  son números reales, y que
son números reales, y que  , y se desea encontrar
, y se desea encontrar  . Un error muy común es "tomar la raíz cuadrada" y deducir que
. Un error muy común es "tomar la raíz cuadrada" y deducir que  . Esto es incorrecto, porque la raíz cuadrada de
. Esto es incorrecto, porque la raíz cuadrada de  no es
no es  , sino el valor absoluto
, sino el valor absoluto  , una de las reglas descritas anteriormente. Luego entonces, todo lo que se puede concluir es que
, una de las reglas descritas anteriormente. Luego entonces, todo lo que se puede concluir es que  , o equivalentemente
, o equivalentemente 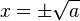 .
. - En cálculo, cuando se prueba que la función raíz cuadrada es continua o derivable, o cuando se calculan ciertos límites, la siguiente igualdad es muy útil (consiste en multiplicar y dividir por el conjugado, véase Binomio conjugado):

- y es válida para todos los números no negativos
 e
e  que no sean ambos cero.
que no sean ambos cero.
- La función
 es continua para todos los números no negativos
es continua para todos los números no negativos  y derivable para todos los números positivos
y derivable para todos los números positivos  (no es derivable para
(no es derivable para  ya que la pendiente de la tangente ahí es ∞). Su derivada está dada por
ya que la pendiente de la tangente ahí es ∞). Su derivada está dada por
- Las Series de Taylor de
 en torno a
en torno a  se pueden encontrar usando el Teorema del binomio:
se pueden encontrar usando el Teorema del binomio:


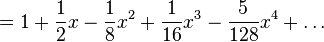
converge para  .
.
Suscribirse a:
Entradas (Atom)